Introduction to Algebra – Growth mindset and map coloring

1.1 Introduction to Algebra

What is Algebra?

Algebra is more than just a series of equations, it is also a way of thinking logically about the world. It is a process that lets us explore the abstract relationships between different things and then provides us with a way to describe those relationships.

We use variables and other symbols as tools to help us express this abstraction in a way that is easier to work with.

Science Says — Everyone Can Learn Algebra!

    • Believe in yourself. Effort, motivation, and resilience will lead to success.
    • People with persevere despite setbacks are more successful.
    • Visualizing and making connections will strengthen your brain.
    • When you learn how to solve new kinds of problems, your brain grows new neurons and you get smarter.
    • Intelligence is learned and not fixed. Your brain actually adapts and rewires itself when you learn new things, and it can
                                                              do so relatively quickly.

What to do if you get stuck:

    • make sure you understand the problem
    • draw a picture
    • if you can’t solve the problem, try to solve a simpler version of the problem
       – use easier numbers
       – keep simplifying the problem until it becomes clear
    • work backwards and ask yourself:
       – what am I trying to find out?
       – what information do I need to know?
       – how do I find that information?
    • ask questions and seek input from others
       – questions help our understanding of the material and can lead us to new insights
       – talk about what you have tried, discuss what you can do next
    • remind yourself that you have overcome setbacks in the past, and you can figure this out

How Mathematicians Think

Although Map Coloring is a topic of Graph Theory, the basic idea is simple and can demonstrate how mathematicians think.

1. Start with a question:

“Have you ever colored in a pattern and wondered what is the smallest number of different colors needed so that no two sections that share a common edge are the same color?”

For example: What is the smallest number of colors you can use to color this drawing?
      Hints: Using numbers to represent each color lets you change your mind.
           Also, remember that having a corner (point) in common is ok.

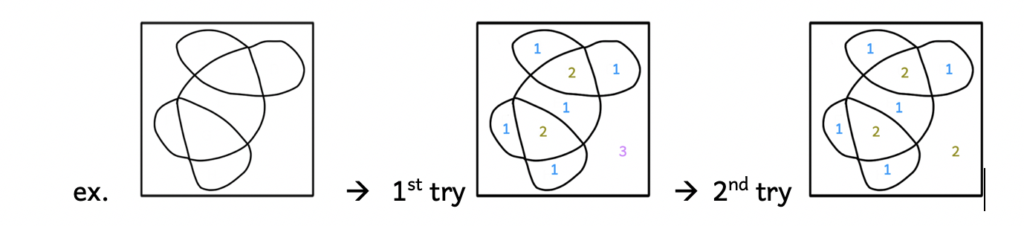
2. It is ok to make mistakes. The processes you use matter.

While trying to find out how many colors are needed and then proving their conjectures (educated guesses), mathematicians went down many wrong paths, but what they learned along the way led to other advancements in mathematics.

3. Draw it out:

Create your own “map.” Color your designs using the smallest number of colors you can.

4. Talk to Others

Discuss the different strategies people used to minimize the number of colors used.

Compare your work. Could you have used fewer colors? Try redoing the design that required the most colors and see if you can color it using fewer colors.

5. Make a conjecture

      of how many colors one needs to color any pattern.

I think all “maps” can be colored using _______ colors.

6. Prove the conjecture: Speed is not the most important thing.

In 1852 Frederic Guthrie (a map maker and mathematician) noticed he only needed 4 colors to color any map and wondered if this was true for all maps. It seemed like a simple idea, but sometimes simple ideas can be very hard to prove. The Four-Color Map Theorem, was not proven until 1976, 124 year later. (This was the first time a computer was used to prove a major mathematical theorem.)

7. Challenge yourself

Redo a graph that took more than four colors, or try and create a graph that requires 5 colors.

Talk about procedures and share ideas