Rewriting Linear Equations in Standard Form

There are times when you may want to rewrite linear equations in standard form. In this video we will rewrite three equations and then graph one of them. The characteristics and advantages of standard form will also be discussed.

Remember the equation needs to be in the form: $Ax+By=C$

where $A$, $B$ and $C$ are integers, and $A$ is positive.
When an equation written in standard form it is easier to find
the x and y-intercepts.

On your own:

1. Write $\color{blue}{3y-8=5x+2}$ in standard form and then graph the equation.
2. Write $\color{blue}{0=2(2x-5y+1)}$ in standard form.
3. Write $\color{blue}{y=\frac{4}{5}x-\frac{2}{3}}$ in standard form.

Solutions:

1. Original problem:    $\color{#d8608c}{3y-8=5x+2}$
Remember the number in front of $x$ needs to be positive. To do that we need to multiply
each term by $-1$.

$$
\begin{align*}
3y-8\color{#d8608c}{+8} &= 5x+2\color{#d8608c}{+8} \\
3y &= 5x+10\\
\color{#d8608c}{-5x}+3y &= 5x\color{#d8608c}{-5x}+10\\
\color{#d8608c}{-1}(-5x+3y &= 10) \\
\color{#d8608c}{5x-3y} &= \color{#d8608c}{-10}
\end{align*}
$$
To graph the equation we will make a table of points starting with
the x- and y-intercepts.

$$ \begin{array}{c|c} x & y\\ \hline 0 & 3\frac{1}{3}\\ \hline -2 & 0\\ \hline 1 & 5\\ \hline 4 & 10\\ \hline \end{array} $$

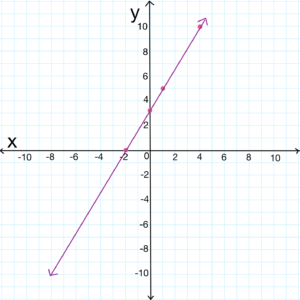2. Original problem:    $\color{#09a067}{0=2(2x-5y+1)}$
You should simplify you equation if you can. In this case all the terms are divisible by 2.

$$
\begin{align*}
0 &= \color{#09a067}{4x-10y+2}\\
\color{#09a067}{-2} &= 4x-10y\\
\\[1px]
\frac{-2}{\color{#09a067}{-2}} &= \frac{4x}{\color{#09a067}{-2}}-\frac{10}{\color{#09a067}{-2}}\\
\\[1px]
\color{#09a067}{-1} &= \color{#09a067}{2x-5y} \quad or \quad \color{#09a067}{2x-5y=-1}
\end{align*}
$$
3. Original problem:    $\color{purple}{y=\frac{4}{5}x-\frac{2}{3}}$
Remember fractions are not allowed in standard form, to clear the fractions we will need to multiply each term by $15$.

$$
\begin{align*}
y\color{purple}{*15} &= \frac{4}{5}x\color{purple}{*15}-\frac{2}{3}\color{purple}{*15}
\\[1px]
15y &= 12x-10\\
15y\color{purple}{+10} &= 12x-10\color{purple}{+10}\\
15y+10 &= 12x\\
15y\color{purple}{-15y}+10 &= 12x\color{purple}{-15y}\\
\color{purple}{10} &= \color{purple}{12x-15y} \quad or \quad \color{purple}{12x-15y=10}
\end{align*}
$$