Linear Equations and Graphing
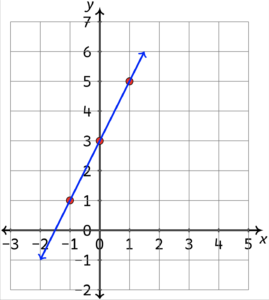
In this video we look at how to graph the equation y = 2x + 3. This is a linear equation, since when it is graphed it will form a straight line. The video provides a detailed explanation of how to graph the solution by first creating a table of coordinates.
How to graph a linear equation by first creating a table of coordinates.
Graph: $2x+3=y$
Let’s start by making a table of some of the possible values for $x$ and $y$.
When you choose a value for one of the variables, you can determine the value of the other, and since there are an infinite number of choices for x, there will be an infinite number of solutions. When it makes sense, choose a positive value, zero, and a negative value.
Next we need to graph the points. Since this is a linear equation, all the points will fall on the same line.
If for the points you plotted do not line up, try graphing a fourth point and that should help you find your error.
Your Turn:
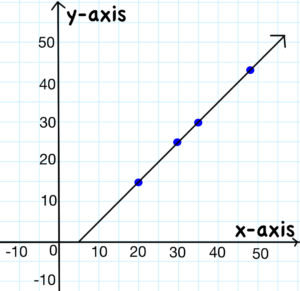
Morgan had $x$ dollars at the beginning of the day. He spent $y$ dollars on clothes. At the end of the day he had $5$ dollars left. Write an equation to represent this situation and create a graph to show the possible values for the amount he had at the start and how much he spent.
Solution:
The equation to solve this is $\color{blue}{x-y=5}$.
Because Morgan did not spend more than he had all the solutions will have to be positive, and the graph will be in quadrant I.
Let’s start by making a table.
$$
\begin{array}{c|c|c|c}
x & x-y=5 & y & \color{blue}{(x,y)}\\
\hline
20 & 20-y=5 & 15 & \color{blue}{(20,15)}\\
\hline
30 & 30-y=5 & 25 & \color{blue}{(30,25)}\\
\hline
35 & 35-y=5 & 30 & \color{blue}{(35,30)}\\
\hline
48.50 & 48.50-y=5 & 43.50 & \color{blue}{(48.50,43.50)}\\
\hline
\end{array}
$$
Remember: if you choose a value for one of the variables, you can determine the value of the other, and since there are an infinite number of choices for x, there will be an infinite number of solutions.
What does the coordinate (0,5) represent?